La ripetizione periodica di stati identici nei sistemi dinamici secondo Poincaré
Se avete l’impressione di tornare spesso sui vostri passi senza neanche farlo apposta, non siete i soli. Probabilmente il matematico francese Poincaré era particolarmente affetto da questa forma di déjà vu. Tanto da enunciare il Teorema del ritorno: a volte non importa da dove cominci, sei destinato a tornarci di nuovo. Per comprendere a fondo il risultato di Poincaré e i suoi corollari, dobbiamo parlare la sua lingua. Non il francese: la matematica.
Cominciamo introducendo il concetto di sistema dinamico, già incontrato nell’uscita 18 de La Tigre di Carta. Diamone qui una caratterizzazione un po’ più formale. Possiamo pensare a un sistema dinamico come a uno strumento matematico per descrivere, magari anche solo qualitativamente, tutte le evoluzioni possibili di un sistema fisico o meccanico: dal movimento di una pallina dentro una ciotola a quello dei corpi celesti attorno a una stella, da alcune palle su un tavolo da biliardo al movimento delle molecole di gas in una stanza. Come possiamo formalizzare una tale vastità di possibili circostanze nella maniera più agevole? Abbiamo visto nell’articolo del numero 19 che i due strumenti alla base dell’edificio matematico sono gli insiemi e le funzioni (o mappe) tra insiemi. Ebbene, per non complicare le cose, utilizziamo proprio questi due “piedi di porco” matematici. Diciamo che gli stati possibili del nostro sistema meccanico (esempio: tutte le possibili posizioni e velocità di una pallina in una ciotola) sono elementi di un insieme, chiamiamolo M. Poi descriviamo l’evoluzione dinamica del sistema tramite una funzione f che mappa ogni stato del sistema nello stato successivo seguendo la dinamica. La dinamica è dunque rappresentata da questa f, che mappa M in M stesso: f prende ciascun possibile stato m∈M (un elemento di M) e lo mappa nel suo evoluto f(m)∈M (anch’esso un elemento di M, cioè uno stato possibile del sistema). Per trovare poi l’evoluzione ancora successiva, quindi per conoscere lo stato del sistema al “tempo” successivo, dobbiamo semplicemente riapplicare f all’elemento f(m), e così via: otterremo così la cosiddetta orbita del sistema dinamico, un fluire di stati governato dalla dinamica. Per quanto riguarda la funzione f, chiamata spesso flusso, si noti che la sua forma esplicita dipenderà dalle leggi fisiche che si considerano, ad esempio la gravitazione universale di Newton nel caso dei pianeti attorno alla stella. A questa si potrebbe aggiungere, per esempio, la correzione dovuta alla Relatività generale di Einstein, ma la potenza della formalizzazione matematica sta nel fatto che, una volta ridotto il problema in una forma astratta coi semplici strumenti matematici M e f, la specificità delle leggi fisiche passa quasi in secondo piano. Non siamo più legati al problema concreto, ma possiamo permetterci di spaziare liberamente con la fantasia.
È questo tipo di fantasia e genialità che emerge dalla memoria di Henri Poincaré intitolata Sur le problème des trois corps et les équations de la dynamique, depositata in occasione della gara matematica indetta da Oscar II Re di Svezia e di Norvegia (per un breve resoconto di questo episodio, si veda il numero 3 della Tigre). In questa memoria Poincaré discute per la prima volta del suo Teorema del ritorno, o Teorema di ricorrenza.
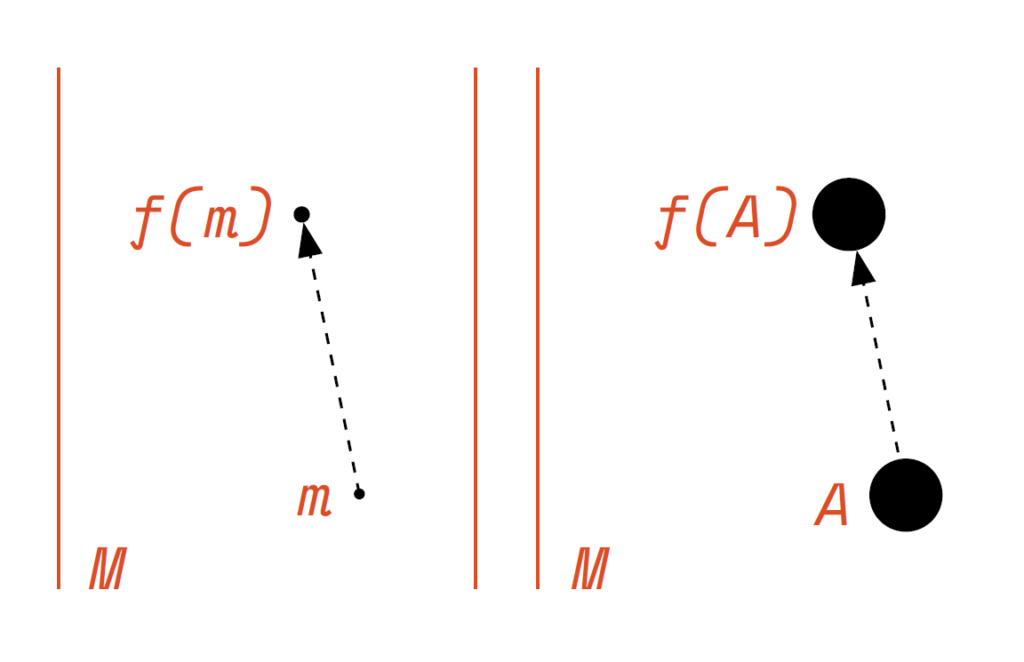
Cominciamo ricordando che la funzione f prende ciascun elemento di M e lo mappa nel suo evoluto f(m), anch’esso un elemento di M (Figura 1, sinistra). Possiamo allora anche immaginare come f agisce su un sottoinsieme A di M, ovvero su una regione contenuta in M: essendo A una sotto-collezione di stati del sistema dinamico, f prenderà A e lo mapperà in un altro sottoinsieme di M, che possiamo indicare con f(A). In altre parole, stiamo seguendo la dinamica non di un solo stato, ma di tutta una regione, una “nuvola” di stati iniziali, e stiamo immaginando come questi fluiscono seguendo la dinamica (Figura 1, destra). Poincaré assume ora due ipotesi: la prima è che l’insieme M abbia un volume[1] finito; la seconda è che la funzione f “preservi il volume”, ovvero sia tale che il volume dell’insieme f(A) sia sempre uguale a quello dell’insieme A di partenza. Il suo Teorema del ritorno afferma allora che sotto queste ipotesi, per ogni “regione” A di M (ovvero una sotto-collezione di stati del sistema dinamico), per quanto piccola essa sia, esistono delle orbite (cioè queste evoluzioni del sistema dinamico) che passano per A infinite volte. Equivalentemente detto: il sistema ritorna arbitrariamente vicino al dato di partenza iniziale in un lasso di tempo finito (detto tempo di ricorrenza di Poincaré).
Facciamo subito un esempio per “toccare con mano” il significato del Teorema di ricorrenza. Consideriamo per esempio una palla che si muove liberamente su un tavolo da biliardo “matematico”, ovvero senza attrito (e senza buche!). Discuterò sotto perché in questo caso le ipotesi del teorema sono avverate. Il teorema afferma che, nonostante possa essere estremamente difficile calcolare l’evoluzione della palla, possiamo stare sicuri che essa tornerà arbitrariamente vicina al punto di partenza in un tempo finito. Non solo: lo stesso vale indipendentemente dalla forma del tavolo!

Tutto questo sembra un po’ “matemagico”. Per capirci meglio, possiamo rivisitare il Teorema considerando la questione dal punto di vista opposto. Riprendiamo il nostro insieme arbitrario A dell’enunciato del teorema. Consideriamo l’insieme dei punti di A che ricadono dentro A un numero finito di volte dopo ripetute applicazione del flusso f, ma che poi non ci ritornano mai: tale insieme viene chiamato wandering set di A (dall’inglese to wander ovvero “vagare”, “divagare”). Il teorema afferma dunque che, sotto le stesse ipotesi date prima, il wandering set di A ha volume nullo.
Usando questa formulazione, e tenendo in mente l’esempio della palla da biliardo, diventa chiaro cosa debba saltare per far sì che il teorema non sia più valido. Se consideriamo un tavolo anche perfettamente rotondo ma con attrito, e indirizziamo la palla dal centro verso il bordo, essa rimbalzerà e ripasserà per il centro del tavolo ma dovrà per forza rallentare e fermarsi, non necessariamente vicino al punto di inizio. L’ipotesi della conservazione del volume emerge dunque come una traduzione matematica del concetto fisico di conservazione dell’energia meccanica, valida per i sistemi cosiddetti conservativi. In effetti, un noto teorema di Liouville assicura che, dato un sistemo meccanico conservativo, il flusso f conserva il volume. Quando invece un sistema dinamico ha dei wandering set di volume non nullo, ci sono dei sottoinsiemi che inesorabilmente vagano via dallo stato iniziale, cioè il sistema è soggetto a qualche tipo di dissipazione (come ad esempio l’attrito).
Ma le sorprese non finiscono qui. Torniamo al caso del biliardo puramente conservativo, ovvero senza attrito e senza buche, ma questa volta consideriamo non una sola pallina ma un intero set da Palla 8, dalla bianca alle piene alle rigate. Il teorema affermerebbe dunque che, in mancanza di attrito, qualsiasi sia il colpo iniziale inferto alla pallina bianca (la cosiddetta spaccata), tutte le palline ritornerebbero in un tempo finito in una posizione essenzialmente indistinguibile da quella iniziale! Questo tipo di ragionamenti è in forte contraddizione con i risultati della termodinamica, i quali prevedono una sorta di direzionalità intrinseca nell’evoluzione dell’universo che si potrebbe descrivere come rettilinea, mentre il risultato di Poincaré sembrerebbe indicare una natura necessariamente circolare del flusso del tempo. Purtroppo, mi sono dilungato già abbastanza per occuparmi di queste tematiche; chi fosse interessato, tuttavia, può dare un’attenta lettura all’articolo di Fisica!
Note
[1] Piccolo pit-stop tecnico: sto assumendo di poter definire una nozione di volume per M e per opportuni suoi sottoinsiemi, ovvero di avere una cosiddetta misura. Questa è una delle tante possibili strutture matematiche che possono essere fabbricate a partire dagli insiemi, come accennato nell’articolo del numero 19. La questione della misura è di per sé estremamente interessante ma esula dall’argomento di questo articolo; ho parlato brevemente di questo tema nel numero 20.




