Dentro la “B” di Benoît B. Mandelbrot, l’uomo che ha definito i frattali
… «la materia è musica solidificata»: a volte la Matematica è realtà idealizzata ed elevata all’astrazione. Sembra questo il caso dell’opera del matematico polacco Benoît B. Mandelbrot sulla ricorsività e l’imprevedibilità nelle forme naturali, e del suo studio ispirato dalle forme auto-simili, che egli descrisse e generalizzò con il concetto di frattale. I frattali sono spesso considerati sinonimi della mise en abyme, ma possono in realtà essere oggetti molto più versatili e ricchi. Per una definizione più corretta, si potrebbe dire che i frattali sono in generale forme geometriche che si rifiutano di diventare più semplici e “lisce” quando vengono analizzate su scale sempre più piccole, come passando dall’occhio nudo a usare una lente di ingrandimento fino a usare un microscopio. È questo l’approccio geniale di Mandelbrot elaborato nel suo libro del 1975 intitolato Les objets fractals: forme, hasard et dimension.
La definizione matematica di frattale di Mandelbrot è un po’ complicata, e cercherò di darla qui in una versione estremamente intuitiva. Essa si basa su due concetti, che vogliono descrivere come sia possibile assegnare a una forma geometrica delle “dimensioni” diverse. Abbiamo tutti imparato che un punto è 0-dimensionale, un segmento è mono-dimensionale, un quadrato è 2D e un cubo è 3D; ma cosa significa questo veramente? Introdurrò due “dimensioni”, che chiamerò “dimensione di disegno” e “dimensione di riscalamento”, utilizzando proprio queste semplici forme che conosciamo tutti molto bene: il punto, il segmento, il quadrato e il cubo. Tra l’altro, queste figure geometriche contengono (e anzi, sono proprio divisibili in) copie esatte di se stesse, solo in formato sempre più piccolo (vedi Figura 1), pur non essendo frattali! Questo mostra che la tipica definizione di frattale facente riferimento alla pura e semplice mise en abyme non è esattamente precisa, e che la pedanteria di Mandelbrot è del tutto motivata. Quindi, passerò a descrivere un oggetto matematico interessantissimo che è davvero un frattale.
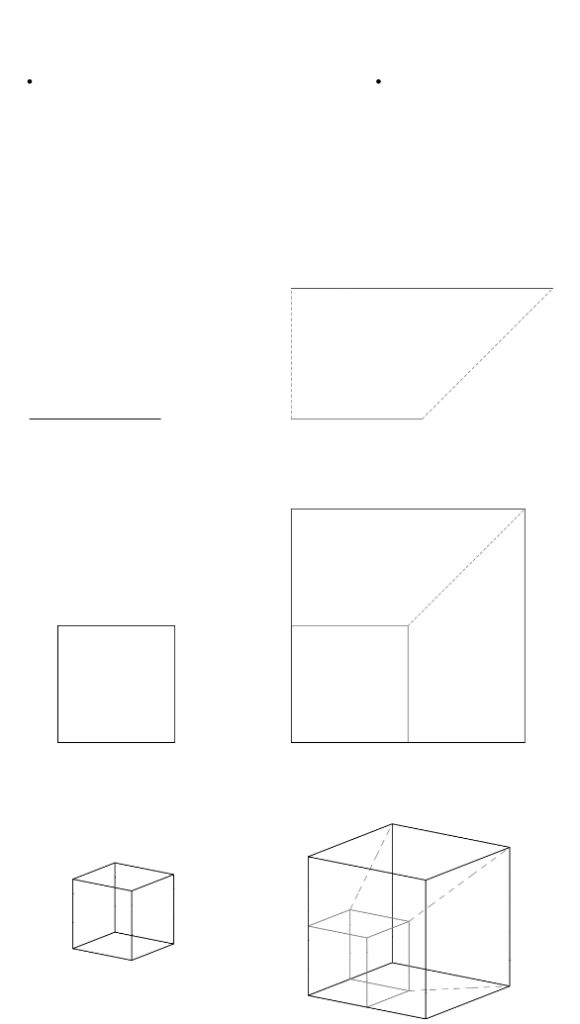
Possiamo definire intuitivamente la “dimensione di disegno” di una figura geometrica, più propriamente detta dimensione topologica, nella seguente maniera. Se la figura è fatta di singoli punti, un po’ come un “unisci i puntini” della Settimana Enigmistica, diciamo che ha dimensione topologica 0. Se la figura è fatta di curve, nel senso che per rappresentarla verrebbe naturale usare del sottile filo di ferro, la dimensione topologica è 1. Se la figura è composta da facce e potremmo ritagliarla da un foglio di carta, la dimensione topologica è 2. Se potremmo chiedere a un bambino di darle forma con del pongo, la dimensione topologica è 3. Questa non è evidentemente una definizione matematica pulita pulita (anzi, ammetto io stesso che non porta necessariamente alla vera dimensione topologica di alcune figure complicate), ma nei casi che consideriamo qui, sarà sempre abbastanza evidente qual è la dimensione topologica. Ad esempio, il singolo punto, segmento, quadrato e cubo hanno come ci aspettiamo dimensioni topologiche rispettivamente 0, 1, 2 e 3.
Veniamo ora alla “dimensione di riscalamento”, detta in gergo dimensione di Hausdorff, che ancora una volta presenterò di maniera intuitiva. L’idea è essenzialmente di vedere quante copie della nostra figura originale otteniamo quando la riscaliamo o “zoommiamo” uniformemente in tutte le direzioni. Con “zoommare” intendo un po’ quello che facciamo col pollice e l’indice sullo schermo di uno smartphone per vedere meglio una foto: la stiriamo uniformemente in tutte le direzioni, come mostriamo nella Figura 1. Se consideriamo un punto matematico idealizzato, pensandolo facente parte di una figura di un “unisci i puntini”, l’idea è proprio che se anche riscalo tutta la figura di un certo fattore, a esempio un fattore 2, il punto di per sé rimane in realtà immutato e non viene allargato; rimaniamo dunque con il singolo punto di partenza. Se invece consideriamo un segmento, e lo riscaliamo allargandolo di un fattore 2, allora è evidente che abbiamo ottenuto esattamente 2 copie di quello di partenza. Se riscaliamo un quadrato espandendolo di un fattore 2, ogni suo lato ha raddoppiato di lunghezza ma otteniamo un quadrato che può essere visto come composto da 4 copie del quadrato di partenza. Infine, riscalando un cubo di un fattore 2, otteniamo un cubo più grande che è composto da 8 cubi di partenza. Quello che vediamo è che abbiamo un fattore di scala s (sempre 2 nei casi precedenti) e un numero di copiosità n (uguale a 1, 2, 4, e 8 nei rispettivi casi), e ci chiediamo che relazione c’è tra s e n nel caso del segmento, del quadrato e del cubo. Chiunque si ricordi le formule per l’area di un quadrato e il volume di un cubo di lato s, si sarà già accorto che la relazione cercata ha la forma sd = n, dove il numero d è proprio la “dimensione di riscalamento” che andiamo cercando: nel caso di un punto la “dimensione di riscalamento” è 0 perché 20 = 1 (l’abbiamo riscalato di 2, abbiamo ottenuto 1 copia), nel caso di un segmento, è 1 perché 21 = 2 (l’abbiamo riscalato di 2, abbiamo ottenuto 2 copie), nel caso di un quadrato è 2 perché 22 = 4 (l’abbiamo riscalato di 2, abbiamo ottenuto 4 copie), nel caso di un cubo è 3 perché 23 = 8 (l’abbiamo riscalato di 2, abbiamo ottenuto 8 copie).
Nonostante “dimensione di disegno” e “dimensione di riscalamento” siano definite in modi ben diversi, abbiamo concluso che coincidono per un punto, un segmento, un quadrato e un cubo. E, come abbiamo già detto, questi non sono frattali (anche se contengono copie esatte ma riscalate di se stessi, cosa di cui ci siamo serviti per calcolare la loro dimensione di Hausdorff). Ebbene, la definizione di Mandelbrot è: un frattale è una figura che ha una dimensione di Hausdorff diversa (più grande) dalla sua dimensione topologica.
Per fornire un esempio concreto, mi sento in dovere di estrarre dal cappello un oggetto puramente matematico che ha un interesse pratico nella disciplina avendo innumerevoli proprietà interessanti: l’insieme di Cantor. Questo è un insieme di punti costruito nella seguente maniera. Si considera un segmento, lo si divide in tre parti uguali e si butta via la parte di mezzo. Con le due estremità di segmento rimanenti, si ripete la stessa procedura: le si divide ciascuna in tre parti uguali e si buttano via le parti di mezzo. Si continua così, come mostrato nella Figura 2 per le prime 6 iterazioni. L’insieme di Cantor si ottiene operando così infinite volte. Quali sono le dimensioni topologica (cioè di disegno) e di Hausdorff (cioè di riscalamento) di questo insieme? Per come l’insieme è costruito, l’insieme di Cantor è costituito da soli punti[1], quindi la sua dimensione topologica è 0 (si utilizza addirittura il nome evocativo di polvere di Cantor). Poi, è evidente che riscalare l’insieme di Cantor allungandolo di un fattore 3 equivale a cominciare da un segmento di partenza 3 volte più lungo, e siccome stiamo buttando via il terzo di mezzo otteniamo esattamente 2 copie dell’insieme di Cantor di partenza (come indicato dalle linee grigie a tratti della Figura 2). Allora possiamo calcolare la dimensione di Hausdorff risolvendo l’equazione 3d = 2, che dà come risultato d = log32 = 0,63… Questo numero è strettamente più grande di 0, la dimensione topologica dell’insieme di Cantor, e dunque quest’ultimo è un frattale secondo Mandelbrot.

L’insieme di Cantor è un caso matematico da manuale di mise en abyme, di un oggetto che contiene copie di se stesso. Questo ci ha permesso di calcolare molto rapidamente la sua dimensione di Hausdorff perché è sufficiente risolvere un’equazione la forma sd = n con s e n ottenuti tramite semplici considerazioni grafiche. Ma la definizione di frattale di Mandelbrot è molto più generale: non è necessario che un oggetto sia auto-simile per essere un frattale. Di fatto, la proprietà che rende l’insieme di Cantor un frattale è il fatto che a qualunque livello di “zoom” riotteniamo una figura che è altrettanto ricca che la figura iniziale: è questo che rende la dimensione di Hausdorff (che descrive come varia la complessità dei dettagli dell’insieme rispetto ai cambi di scala) maggiore di quella topologica (che cattura la geometria delle componenti dell’insieme a sé stante). Ma in generale non è necessario che a livelli di “zoom” sempre maggiori sia la figura di partenza a ricomparire: possono essere altre figure magari un po’ diverse ma comunque altrettanto complicate e articolate.
È questa l’idea innovativa di Mandelbrot: a guardarle sempre più da vicino, alcune figure non perdono di definizione e di dettaglio, ma riservano delle sorprese nascondendo al loro interno ricche strutture sempre più fini, in ribellione alla locuzione divide et impera. Per cosa sta la B in Benoit B. Mandelbrot? Sta per Benoit B. Mandelbrot. E come molte intuizioni puramente matematiche, anche questa porta con sé un valore pratico fondamentale, chiudendo il cerchio che abbiamo aperto all’inizio. Molti oggetti e forme materiali, dal comune broccolo romanesco alla costa della Gran Bretagna (o qualunque altra linea costiera) agli anelli di Saturno sono frattali secondo Mandelbrot. E sono frattali addirittura quelle strutture che ci permettono di vivere e di respirare, come i vasi sanguigni e polmonari, come quelli di un’immensa creatura degli abissi che ha ispirato così filosofi e romanzieri, come John Milton, il quale nel Paradise Lost dice…
Note
[1] Piccola dimostrazione. Tanto per cominciare, l’insieme di Cantor contiene qualche punto: ad esempio le due estremità del segmento iniziale non vengono mai eliminate. Poi, esso non contiene nessun segmento, ma solo singoli punti. Infatti a ogni passo della procedura di costruzione si mantengono solo i 2/3 della lunghezza precedente, e moltiplicando 2/3 per se stesso un numero sufficiente di volte si ottiene una quantità arbitrariamente piccola. Quindi nell’insieme di Cantor non può essere contenuto nessun segmento, perché ogni segmento ha una lunghezza strettamente maggiore di 0.



