di Gabriele Pichierri
///
Spesso sentiamo parlare di cifre enormi più grandi di noi, ma anche i numeri piccoli possono causare grosse difficoltà. Non solo nelle menti dei maggiori matematici, ma nelle orbite stesse dei pianeti intorno al Sole. Come possono numeri tanto piccoli influenzare i moti di massicci corpi celesti?
I matematici hanno a che fare con l’infinitamente piccolo e l’infinitamente grande ogni giorno. Abbiamo parlato di quanto più piccolo ci possa essere, lo zero, nell’ultima uscita, e l’I Ching non sembra volerci portare troppo lontano: forse è il caso di seguire il consiglio e rievocare alcune tematiche passate. Appena ho saputo il titolo di questo numero, mi è venuto in mente un problema che risulta una naturale continuazione di molti argomenti già affrontati in precedenza. La questione è abbastanza tecnica ma l’occasione è ghiotta per mostrare i comportamenti dei numeri piccoli che i matematici devono tenere in considerazione: giudicate voi se nel mio piccolo sono riuscito ad affrontare la sfida.
Secondo Poincaré (chi si fosse dimenticato di chi stiamo parlando dia uno sguardo all’articolo del numero 3), il problema fondamentale della dinamica è il seguente: si considera un sistema su cui sappiamo tutto, detto integrabile, e gli si aggiunge una piccola perturbazione. Un esempio pratico è il sistema Terra-Sole, ben descritto dalle leggi di Keplero, al quale si aggiunge la perturbazione dovuta a Giove. La domanda è se anche il sistema perturbato non sia in realtà integrabile, ovvero se riusciamo a dire tutto su come evolve. Che questo in generale non sia possibile, a causa di comportamenti caotici, l’aveva scoperto proprio Poincaré, come abbiamo visto nella terza uscita, e il motivo è essenzialmente già descritto nella ivi citata memoria per il premio del re di Svezia (per chi ne capisce di sistemi dinamici o per chi afferra la nomenclatura, sto parlando del Teorema di non esistenza degli integrali primi).
Si potrebbe però considerare la perturbazione non nella sua totalità, ma solo fino a un certo ordine di grandezza, e confidare che quello che stiamo trascurando sia piccolo abbastanza da non avere grosse conseguenze sull’evoluzione del sistema. Senza entrare nelle questioni tecniche, l’idea è di rappresentare il sistema tramite un’espressione che sia una somma di due termini, dove il primo rappresenta il sistema integrabile, e il secondo la perturbazione. Siccome quest’ultima è molto piccola, ci sarà un piccolo parametro che ci dà un’idea di quale possa essere il suo ordine di grandezza; ad esempio, nel nostro sistema solare si può considerare il rapporto tra la massa del pianeta più massiccio (Giove) e la massa del Sole, che è dell’ordine di un millesimo, 0.001 = ε. A questo punto entra in gioco una proprietà dei numeri piccoli: se si moltiplicano tra loro il risultato è ancora più piccolo. Ad esempio, ε × ε = ε² è 0.000001, ε³ è 0.000000001 ecc. Le potenze di ε sono ben adatte a fare da “legenda” per gli ordini di grandezza dei diversi contributi della perturbazione: il contributo di ordine di grandezza “un millesimo” avrà attaccato un ε, e così via.
Quindi possiamo “spacchettare” il termine che rappresenta la perturbazione in un primo addendo di ordine ε (un millesimo), un secondo addendo di ordine ε², e così via, in linea di principio generando un numero infinito di addendi:
Sistema = [parte integrabile] + [ε × (primo addendo) + ε² × (secondo addendo) + … ].
A questo punto ci ricordiamo della potenza delle costruzioni per ricorrenza, incontrate nel numero 5 della nostra rivista. Cominciamo a considerare la parte integrabile del sistema al quale aggiungiamo non tutta la perturbazione ma solo il primo addendo, di ordine ε. Se riuscissimo a riscrivere questo sistema intermedio in modo tale da “cancellare” il termine ε × (primo addendo) avremmo ottenuto che esso è integrabile, e scriveremmo:
Sistema = [nuova parte integrabile] + [ε² × (secondo addendo) + ε³ × (terzo addendo) + … ];
potremmo procedere così, iterando ad ogni ordine di grandezza, finché…[1] Be’, in generale non possiamo aspettarci di eliminare tutta la perturbazione, il sopracitato Teorema lo esclude. Ma nella pratica che cos’è che fa saltare la costruzione? La risposta si può riassumere così: risonanze e piccoli divisori.
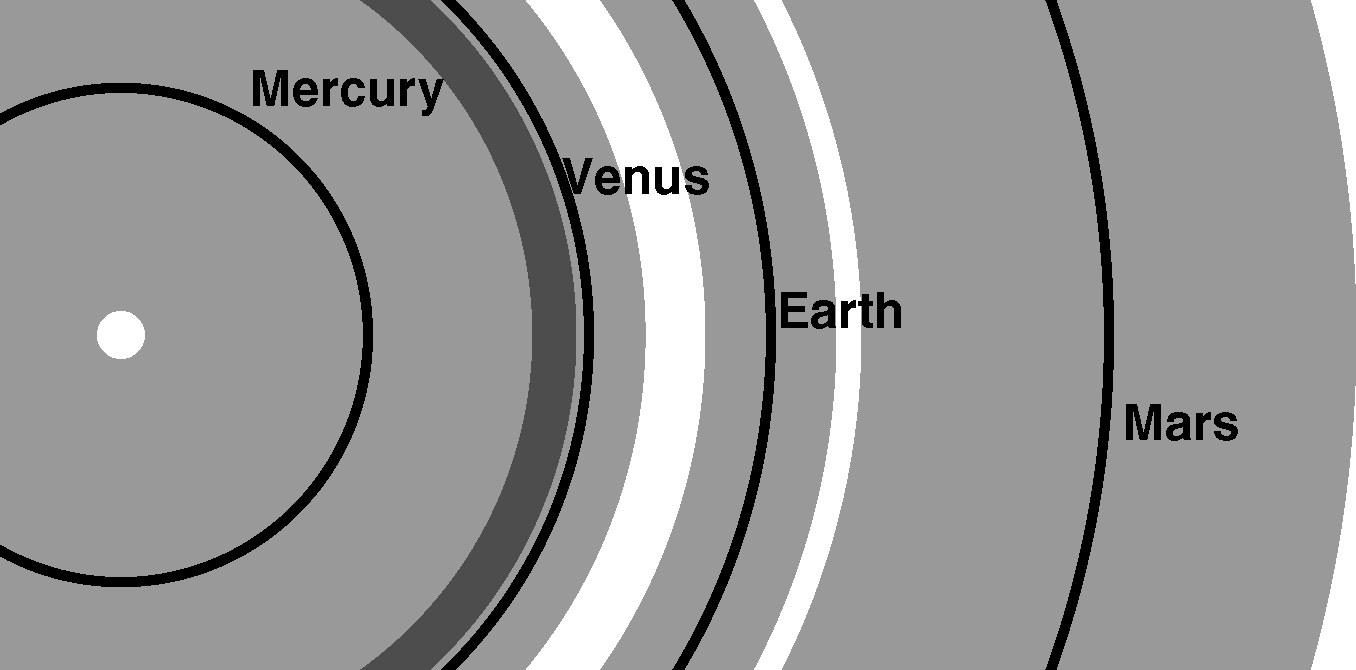
La figura mostra le possibili zone che i pianeti minori potrebbero occupare nell’arco di 5 miliardi di anni; le linee nere corrispondono ad orbite circolari, e le fasce grigie che le circondano denotano tali zone. Si noti come soprattutto Mercurio può occupare una zona molto ampia, tale da sovrapporsi con quella di Venere: in effetti c’è una possibilità di circa 1% che Mercurio impatti con Venere o con il Sole, entro 3-5 miliardi di anni. Si veda l’articolo di J. Laskar.
La parola “risonanze” può forse stuzzicare l’udito più che l’interesse matematico, ma al di fuori dell’armonia musicale esse possono avere effetti catastrofici (si veda ad esempio il ben documentato collasso del Tacoma Narrows Bridge nel 1940), ed è bene trattarle con precisione. In ogni caso, per capire cosa sia una risonanza possiamo sfruttare il senso comune del termine e immaginare di avere due corde che emettono due note, cioè vibrano alle frequenze fondamentali ω1 e ω2 rispettivamente. Come già aveva intuito Pitagora, abbiamo una risonanza quando il rapporto delle due frequenze è un numero razionale (vedi l’articolo 5 della nostra rivista); ad esempio il La4, quello centrale sul pianoforte e avente frequenza 440 Hz, è in risonanza 1:2 con il La5, quello esattamente un’ottava sopra, con frequenza 880 Hz. Più in generale si ha una risonanza quando ω1:ω2 = h:k, dove h e k sono numeri interi; questo lo si può riscrivere “k ω1 − h ω2 = 0”, con h e k interi, seguendo così l’abitudine dei matematici di porre qualcosa uguale a zero. Il perché questo possa creare problemi catastrofici sarà chiaro tra un attimo.
Un’altra buona abitudine dei matematici è quella di risolvere equazioni, e in effetti a ogni passo della costruzione sopra, quando si cerca di “eliminare” un addendo “perturbante” inglobandolo nella parte integrabile (supponendo di aver già trattato tutti gli addendi di ordine di grandezza maggiore), va risolta una cosiddetta equazione omologica, che ha la seguente forma:
a ∙ x = b, (1)
dove x è l’incognita, mentre a e b sono noti, ovvero fissati dal sistema che stiamo considerando; in particolare b è (strettamente legato a) l’addendo “perturbante” che si vuole eliminare allo step in questione del procedimento iterativo. Questa è l’equazione più semplice che esista, e si risolve banalmente dividendo a destra e a sinistra per a, e ciò dà come risultato x = b/a… ma solo se a ≠ 0! Se invece a è nullo non esiste nessun x che moltiplicato per zero dia come risultato b, che è evidentemente non nullo dato che stiamo cercando di cancellarlo. E guarda caso il numero a in questione è legato alle frequenze del sistema integrabile di partenza proprio attraverso espressioni della forma k ω1 − h ω2, così che, quando il sistema esibisce delle risonanze, la nostra costruzione si ferma e la perturbazione non la possiamo cancellare[2].
A questo punto chiunque sia interessato a un’applicazione concreta potrebbe obiettare: noi non sappiamo mai con infinita precisione i valori e le frequenze di un sistema, se non altro per errori di misura possediamo solo intervalli di valori possibili; allora perché non fare i conti con dei valori numerici vicini a quelli misurati e scelti in modo tale da evitare le risonanze? In termini matematici: assumi una non-risonanza e porta avanti i conti. Ebbene, in questo caso le frequenze saranno pure non risonanti, ma sono quasi-risonanti, ovvero k ω1 − h ω2 non sarà proprio zero, ma sarà molto molto piccolo. Posso certamente risolvere le equazioni (1) e ottenere x = b/a, ma qui entra in gioco l’altra faccia della medaglia: quando si divide per un numero piccolissimo, si ottiene un numero molto grande. Risultato: i termini che avevo organizzato per ordini di grandezza sempre più piccoli vengono “amplificati” dai piccoli divisori, e il procedimento iterativo basato sull’organizzazione degli addendi per ordini di grandezza non porta da nessuna parte. I divisori troppo piccoli sono ciò che effettivamente trattiene e inibisce la costruzione che mirava a integrare (cioè risolvere) il sistema perturbato.
Un esempio concreto sono proprio i pianeti più massivi, Giove e Saturno, i quali nelle loro orbite intorno al Sole esibiscono una quasi-risonanza 2:5 che porta a una perturbazione periodica, con periodo di poco più di 900 anni. Concludo dunque questo articolo tornando al nostro sistema solare e alla domanda sulla sua stabilità posta nell’articolo 3. Piuttosto che studiarne la stabilità perpetua, possiamo accontentarci di dominare la dinamica su tempi finiti, ma possibilmente lunghi, tramite variazioni (per nulla banali) del programma brevemente esposto sopra. Si insegue ad esempio una stabilità esponenziale, idea introdotta per la prima volta da J. Moser nel 1955 in uno studio sulla dinamica degli acceleratori di particelle: se la perturbazione è abbastanza piccola, allora il tempo necessario perché il caos provochi un cambiamento sensibile della dinamica cresce esponenzialmente[3]. Per citare J. E. Littlewood, che abbiamo già incontrato nell’articolo 4, «While not eternity, this is a considerable slice of it». Ma che per il sistema solare la perturbazione (l’attrazione mutua tra i corpi celesti) sia davvero “abbastanza piccola” è una questione delicata. Servono misure accurate su tempi molto lunghi, dell’ordine di milioni di anni, per poter apprezzare le variazioni ai moti planetari, delle quali semplicemente non disponiamo. Negli ultimi decenni la ricerca si è spostata sulle simulazioni al calcolatore, che confermano[4] la presenza della dinamica caotica per i pianeti minori, in particolare Mercurio, mentre sembrano indicare una certa stabilità (dell’ordine di decine di miliardi di anni) per i pianeti più massicci. In ultima analisi, la risposta esatta sulla stabilità del sistema solare ancora non la conosciamo, ma i matematici ci stanno lavorando! Quello che è certo è che noi autori e lettori de La Tigre di Carta non abbiamo nulla da temere: la Terra non andrà troppo lontano almeno per le prossime centinaia di milioni di anni.
Note
[1] In gergo si dice che stiamo cercando di scrivere il sistema in una forma normale.
[2] Quello che si farebbe a questo punto è scrivere il sistema in una forma normale risonante, ma non è il caso di entrare nei dettagli.
[3] Antonio Giorgilli, La stabilità del sistema solare: tre secoli di matematica, Matematica, Cultura e Società, Pisa, Edizioni della Normale.
[4] Cito ad esempio il lavoro di J. Laskar dal 1989 a oggi.




