di Amedeo Bellodi
///
Quando il minimo dettaglio domina i fenomeni naturali e ne condiziona l’evoluzione, perdiamo la speranza di poter sapere tutto quel che vorremmo. Ed è caos.
Vi siete mai chiesti cosa passa per la testa a noi redattori quando ci viene comunicato, con adeguati squilli di trombe e rulli di tamburi, l’esagramma estratto per un nuovo numero da preparare? La risposta precisa forse non è il caso di metterla per iscritto qui; confermo piuttosto che è ovviamente necessario librarci in un volo di fantasia, così da scovare in quale modo declinare la profezia dell’I Ching entro la propria area di interesse. Il lavoro non finisce qui: il collegamento con l’esagramma di sviluppo fa sì che io personalmente da astrofisico diventi ogni volta un po’… astrologo, per individuare analogie tra i due temi. Racconto tutto questo non per togliere sacralità alla nostra produzione editoriale, ma anzi svelo questi retroscena per contestualizzare il mio percorso di scrittura, che in questo numero è stato insolito e sorprendente.
Forse un po’ annoiato dall’esagramma estratto (“La forza domatrice piccola” mi ricordava paradossalmente “La potenza del grande” di poche “Tigri” fa), sono rimasto più a lungo a meditare sull’esagramma di sviluppo: “Il mite, il penetrante vento”. Pensai infatti che potesse essere l’occasione adatta per raccontare di meteorologia, una branca della scienza che quotidianamente ci riguarda e di cui troppo spesso ignoriamo le profonde basi fisiche. Non c’è scampo però: a un certo punto avrei dovuto pur ricollegarmi a “La forza domatrice piccola”, ma come fare? In realtà il collegamento era lì, davanti ai miei occhi. L’occasione per illuminarmi è stato il mio ultimo viaggio, con destinazione l’Irlanda. Nelle settimane antecedenti la mia partenza, sono diventato dipendente dai siti web di previsioni meteorologiche: una settimana eccezionalmente di bel tempo, dicevano; poi, a pochi giorni dalla partenza, il cielo di Dublino sembrava aver fatto scorta di nuvole, piogge e temporali. Possibile che nel terzo millennio, pensavo, ancora non abbiamo capacità e tecnologie per avere una miglior precisione riguardante le previsioni meteo con un minimo di preavviso? Che imbarazzo che un fisico si sia posto una domanda simile, dimenticandosi gli insegnamenti di Edward Lorenz.
È il 29 dicembre 1972, alle ore 10 del mattino, presso lo Sheraton Hotel di Boston. Il matematico statunitense Edward Lorenz tiene un seminario alla Conferenza annuale della American Association for the Advancement of Science. Il suo intervento sarà epocale e il titolo vi farà intuire il motivo: “Predictability: does the flap of a butterfly’s wings flying in Brazil set off a tornado in Texas?”[1] ossia “Il battito d’ali di una farfalla in volo in Brasile può innescare un tornado in Texas?”. La cultura di massa ha interpretato l’espressione del cosiddetto “effetto farfalla” come metafora dei momenti, all’apparenza insignificanti, che imprevedibilmente plasmano il destino. L’espressione (presa in prestito da Lorenz dal racconto fantascientifico di Ray Bradbury Rumore di tuono) intendeva in realtà riassumere – seppur provocatoriamente – la tematica cui si era dedicato negli anni. Parafrasando con l’I Ching, la domanda non si chiede altro che: a cosa è soggetto il (ovviamente, mite e penetrante) vento? Ebbene, la risposta che emergeva dal lavoro di Lorenz evidenziava come i fenomeni meteorologici siano “domati”, in un certo qual senso, da una “forza”, che li controlla pur non essendo altro che piccoli dettagli, all’apparenza innocui.
La branca della fisica cui sono a oggi attribuiti i più importanti studi di Lorenz fu inaugurata ufficialmente proprio dal suo articolo[2] “Deterministic non periodic flow” del 1963[3] ed è oggi è nota come “Teoria del caos”. In tale articolo, Lorenz aveva studiato l’evoluzione dinamica dell’atmosfera, con l’obiettivo di ottenere previsioni meteorologiche più accurate sul lungo periodo partendo da una dozzina di parametri fisici forniti. Eppure, Lorenz si accorse che una differenza infinitesimale in uno dei parametri iniziali (aveva arrotondato 0.506127 a 0.506) poteva condurre a evoluzioni incomparabili fra loro. Il battito d’ali di farfalla rappresentato da questo arrotondamento apparentemente modifica le condizioni atmosferiche in una misura trascurabile, ma le intacca inevitabilmente per il futuro a venire. Proprio in questo senso Lorenz definì il caos: «Quella situazione in cui il presente determina il futuro, ma un presente approssimato non determina approssimativamente un futuro». Nella fattispecie, le previsioni meteorologiche, pur poggiando sulle equazioni della fluidodinamica e della termodinamica, che consentono teoricamente di determinare l’evoluzione nel tempo delle grandezze in gioco, produrranno necessariamente risultati solo approssimativi, pur essendo elaborati tramite raffinate tecniche di calcolo eseguite da calcolatori all’avanguardia. Ecco spiegato perché a Dublino mi son dovuto prendere tanta, tanta acqua… a sorpresa.
L’affermazione di Lorenz non finisce qui: la nostra conoscenza rimane limitata da un duplice punto di vista. Da un lato, le nostre previsioni sono condizionate dall’impossibilità di conoscere l’universalità degli eventi che ne influenzano l’evoluzione; dall’altro, lo studio di un fenomeno non può a priori escludere alcuna causa a monte. Certo, non tutti i sistemi ricadono in questa categoria di analisi: una molla è un sistema “lineare”, in quanto a una differenza piccola di condizione iniziale (di quanto tiro la molla stessa) corrisponde una variazione strettamente dipendente nella sua dinamica. Se la molla fosse un sistema complesso e non lineare, come lo sono i sistemi studiati da Lorenz, una piccola, impercettibile differenza dell’allungamento iniziale della molla potrebbe significare che in un caso la molla torni a comprimersi e nell’altro esploda: «La forza domatrice (per quanto) piccola ha riuscita».
Nonostante il pensiero comune, attorno a noi sono molto numerosi i sistemi caotici: dalle nuvole e, più in generale, i fluidi, all’andamento dei mercati finanziari. Questo ci insegna che il pensiero per cui una realtà caotica indichi necessariamente una situazione disturbata, non auspicabile e innaturale, è una visione non corretta: la caoticità di un sistema va piuttosto letta come flessibilità a poter variare con maggior facilità.
Alcuni studi[4] hanno tra l’altro mostrato
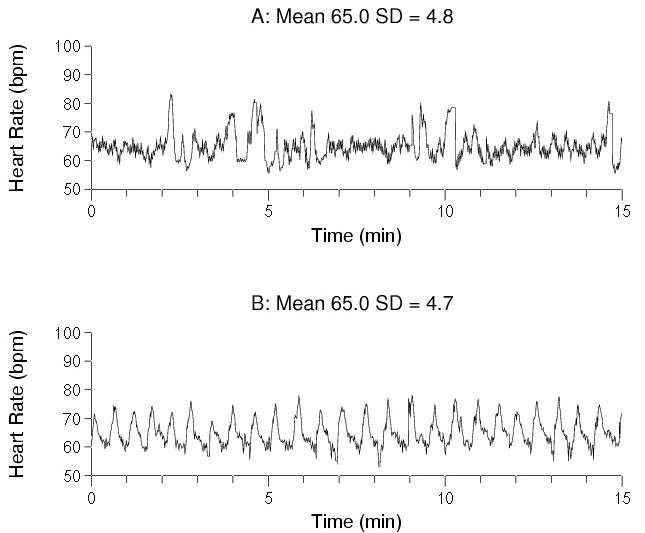
Due serie temporali di frequenze cardiache con uguale valor medio e varianza a confronto. Il caso A appare qualitativamente più complesso e rappresenta un paziente sano. Il paziente B è invece affetto da una sindrome di apnea del sonno di tipo ostruttivo: il suo battito cardiaco presenta delle periodicità più evidenti. Fonte: Physionet.org
come questo tipo di adattabilità sia intrinseca nelle modificazioni del ritmo cardiaco: si è osservato, ad esempio, che la frequenza cardiaca di un individuo sano varia nel tempo con periodicità caotica (vedi Figura 2)[5] e non secondo un normale ritmo sinusale influenzato dai sistemi omeostatici (i meccanismi di autoregolazione degli organismi viventi). L’omeostasi, in questa visione, diventa piuttosto un aggiustamento tra la componente caotica e quella ordinata, così come la malattia è perdita di tale equilibrio nella direzione di maggior “ordine”, nonché minore capacità di assorbire le perturbazioni. Colpiscono a questo punto le parole del generale cinese Sun Tzu: «Con ordine, affronta il disordine; con calma, l’irruenza. Questo significa avere il controllo del cuore». Imprevedibile.
Note:
[1] Il testo dell’intervento è consultabile all’indirizzo http://eaps4.mit.edu/research/Lorenz/Butterfly_1972.pdf
[2] A onor del vero è opportuno segnalare che alcune idee di base erano già presenti negli scritti di altri illustri fisici e matematici dell’Ottocento, tra cui Henri Poincaré.
[3] Edward Lorenz, “Deterministic Nonperiodic Flow”, Journal of atmospheric science, 20, 1963, pp. 130-141
http://journals.ametsoc.org/doi/pdf/10.1175/1520-0469%281963%29020%3C0130%3ADNF%3E2.0.CO%3B2
[4] Cfr. Ary L. Goldberger, “Non linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside”, The Lancet , 247, 1996, pp. 1312-1314.
[5] Per approfondimenti, cfr. Ary L. Goldberger et al., “PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals”, Circulation, 101(23), 2000, pp. e215-e220; http://circ.ahajournals.org/cgi/content/full/101/23/e215





